The Inverse Square Law For Dummies and an Easy Photography Rule of Thumb

I loved physics class in high school. In college, I earned minors in mathematics and engineering. But I was left scratching my head when I first read about how the Inverse Square Law was explained for flash photography.

This explanation, graph, and calculator will make it much easier than many other explanations out there.

Inverse Square Law Explained

The mathematician will tell you that the Inverse Square Law says that the intensity of a force is inversely proportional to the square of the distance from that force. 

You’ll say, what?  

Then the mathematician will attempt to clarify it by writing down the Inverse Square Law formula, Intensity = 1/D².

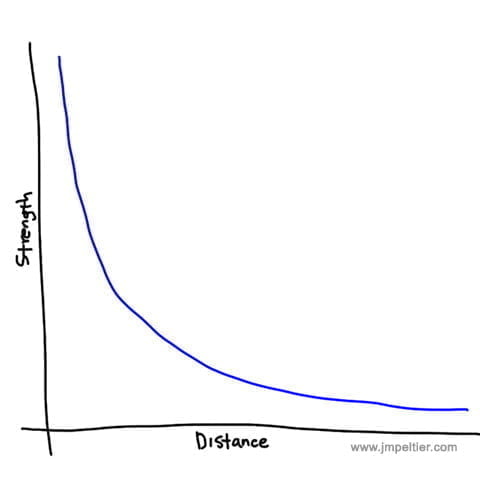
The most basic dummy caveman explanation for the Inverse Square Law is that a force will drastically drop in strength as it moves away from the source and then shallow out. 

That’s the no math explanation, and here’s what the caveman Inverse Square Law graph looks like:

Inverse Square Law Assumptions

The Inverse Square Law is really only 100% accurate when talking about a point source of light, like the period at the end of this sentence. Except that the point light source is so small that it’s theoretical.

Your flash is not a point light source. But when you’re photographing a large group of people, as we’ll see below, practically speaking it’s a point light source because that light is spreading out enough in a manner to more or less follow this “law.”

If you’re using parabolic reflectors or lenses that focus the beam or snoots, that light won’t follow this “law.”

Basic Inverse Square Law Calculator

Play around with the slider to see what happens. Note how the first decrease in strength is by 75%, and next by only 14%.

How does the Inverse Square Law apply to photography?

In photography – which literally means “writing with light” – the Inverse Square Law describes the behavior of light. 

Even though it describes the behavior of all light, it is most useful in flash photography.

For the following Inverse Square Law calculator, we’ll look at a flash with a guide number of 60. Guide numbers are the topic of this post. It’s not important now; know that for this example, you’ll get 100% strength at a distance of 60 meters. 

Play around with the slider to see what happens to the flash power on your subject as you change the distance in 30-meter increments.

Cool, interactive sliders, but what’s a practical photography application for the Inverse Square Law?

Imagine you’re doing a group portrait with one powerful flash. You’ll need your wide lens because they’re fifteen people across. They’re backlit, of course, because nothing is ever easy. You zoom out the flash head and put a shoot-through umbrella in front to ensure coverage of everyone in the photo.

Now, do you place the flash as close as possible to your subjects or back away from them? How do you justify your answer?

Look at the following diagrams.

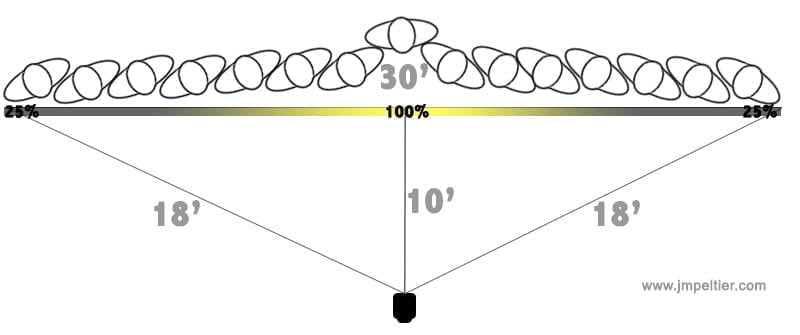
In the first one, we placed our flash 10 feet from the center of the group, which is 30 feet wide. I’ll do the trigonometry for you, but the people on the ends are 18 feet from the flash – almost double that of the center. 

If the people in the center get the proper flash exposure, the people on the ends will only get approximately 25% of that power. They’ll be dark, underexposed by two whole stops.

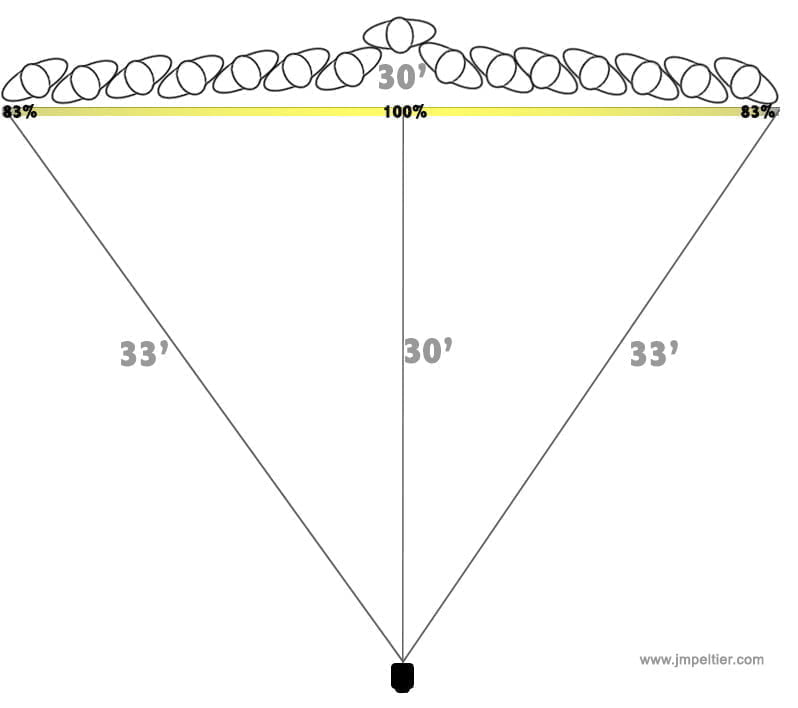
In the second diagram, we move the flash further away from the center of our group. Thirty feet away. Trigonometry tells us that the people on the ends are 33 feet from the flash – barely more than the center. 

The folks on the ends are getting 83% of the light that the people in the center are getting. That’s a difference of only about a third of a stop – a difference imperceptible to most people.

The actual power setting of the flash has nothing to do with the relationship of light hitting all of your subjects. It all has to do with how much the light needs to spread to cover your subjects.

An Easy Inverse Square Law Rule of Thumb

If you want subjects to be evenly lit from one side to the other, crank up the power and make the distance of the flash no less than the width of your subject. The further, the better.

• If the subject is ten feet wide, place the flash at least ten feet from the center.
• If the subject is thirty feet wide, place the flash at least thirty feet away.
• And so on.

Make the triangle look like the second diagram above, not the first.

If you’re looking for a dramatic falloff, like if you want to light up your subject but not the background, dial down the power and put the light source as close as possible to your subject. The closer it is, the sharper the falloff.

After you get that squared away (pun?), it’s just a matter of adjusting your flash power for the proper exposure.

The Inverse Square Law is all about distance, not flash power settings.

Does it all make sense now?

Check out this video from Mark Wallace of AdoramaTV for a walk-through:

Digital Photography One on One: Episode 59: Inverse Square Law

Watch this video on YouTube.